Matemática- NROS. REALES

Números reales.
-Clasificación:

                                             

¿CUÁNDO UN NÚMERO ES DENSO Y DISCRETO?

Números discretos -----> entre un numero y otro no puede haber mas números. 

Ejemplo ---> 1,2,3,4,5,6,7 
Números densos ----->  se le conoce como continuo. Hay infinitos números. Ejemplo 1-1,20- 1,50- 2

SUCESIONES.

¿QUÉ SON? Son un conjunto de números ordenados.

TIPOS.

• Aritméticas: cuando cada término es la suma del término anterior mas un número constante, al que llamamos diferencia y denotamos por d. Es decir: 

                                         an + 1 = an + d

•  Geométricas: cuando cada término es el término anterior multiplicado por un número constante, al que llamamos razón y denotamos por r. Es decir: 

                                          an + 1 = an . r 

       
FÓRMULAS 

SUCESIÓN ARITMÉTICA
Es de la forma
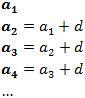Diferencia	Término general
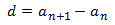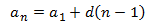Suma de los n primeros términos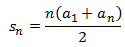
SUCESIÓN GEOMÉTRICA
Es de la forma
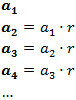Razón	Término general
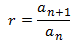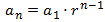Suma de los n primeros términos	Suma de todos los términos

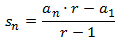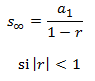EJERCICIOS

•  Dada la sucesión an = (1+1/n)^n

              a) Investiga con tu calculadora y calcula los 10 primeros términos de la sucesión.

              b) ¿Cuánto vale a100? ¿Y a1000?

  

             a) a1 = (1+1/1)^1= 2 

                 a2 = (1+1/2)^2= 2,25                  *LOS TÉRMINOS DE LA SUCESIÓN

                 a3 = (1+1/3)^3= 2,37                              SON POSITIVOS.

                 a4 = (1+1/4)^4= 2,44                  *CADA TÉRMINO ES MAYOR QUE EL 

                 a5 = (1+1/5)^5= 2,48                               ANTERIOR.

                 a6 = (1+1/6)^6= 2,52                  *EL NÚMERO DE N NO PASA EL 3.                 

                 a7 = (1+1/7)^7= 2,54

                 a8 = (1+1/8)^8= 2,56

                 a9 = (1+1/9)^9= 2,58

                 a10 = (1+1/10)^10= 2,59 

       

            b) a100= (1+1/100)^100= 2,70

                a1000= (1+1/1000)^1000= 2,71

PERÍMETRO Y ÁREA



Perímetro ----> Suma de los lados.

EJEMPLO

EJERCICIO DE ÁREA.

• Encuentra el valor del área blanca sabiendo que el área del rectángulo gris es 18 (raíz de 3).

EJERCICIO DE PERÍMETRO.

• De una hoja rectangular se cortan dos triángulos isósceles de 4cm^2 de área. ¿Cuál es el perímetro de la cartulina restante?

  

PROPIEDADES DE LAS RAÍCES → Es distributiva en la multiplicación

               ↓                                  ↘  

                                                   No es distributiva en la suma                                                 

Raíz de raíz, se multiplican

los índices. No se suman